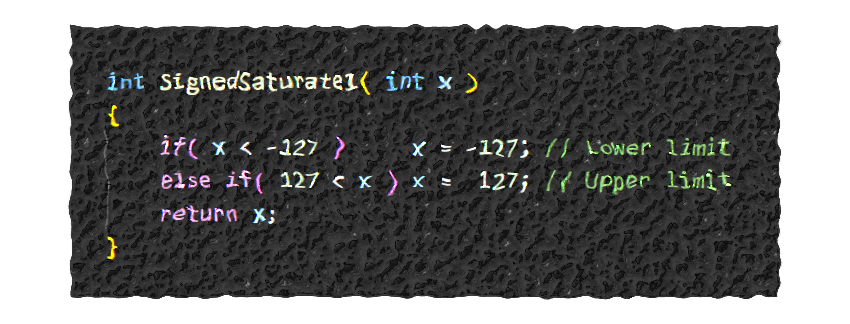
Single-path code, or branchless code, has been an important development in performance computing. It turns out to be even more interesting in the domain of hard real-time, embedded systems. In this third of three articles, let us see what modern compilers do to reduce the number of taken branches on a given code path.

Saturation

The ability of a compiler to surprise the user of a high-level programming language is emphasized by the following example. This is based on a real example, where the control algorithms required that results of integer arithmetic be saturated to symmetric ranges, such as -15 to +15, or -127 to 127. Always the limit was two to the power of n minus one. I asked why they had not exploited the Arm SSAT instruction, and they patiently explained that SSAT performs an asymmetric saturation, for example in the range -128 to +127. And that this made it impossible to use SSAT, they claimed. Rather, they wrote code like SignedSaturate1.

1
2
3
4
5
6
int SignedSaturate1( int x )
{
    if( x < -127 )     x = -127; // Lower limit
    else if( 127 < x ) x =  127; // Upper limit
    return x;
}

As we observed in the previous article, and although it was not the case with the compiler in this particular project, the current Arm CLANG compiler actually does generate branchless code from this example, first using a conditional instruction to truncate on the lower limit, and then a second conditional instruction to truncate on the upper limit.

But this overlooks the fact that SSAT does nearly the correct operation. Only one value needs to be corrected. And the compiler does recognize C code that exactly corresponds to SSAT, translating it as SSAT. So, the following C code actually generates one instruction fewer. (And one of those instructions is unnecessary and would most likely be elided if the function were inlined, as was the case in the real project.)

1
2
3
4
5
6
7
int SignedSaturate2( int x )
{
    if( x < -128 )     x = -128; // Lower limit minus 1
    else if( 127 < x ) x =  127; // Upper limit
    if( -128 == x )    x = -127; // Correct lower limit
    return x;
}

At this point, you might feel that, since we want to exploit the SSAT instruction, we should just use a compiler intrinsic to generate that instruction. There are two major advantages to avoiding an intrinsic function:

1. Partial evaluation: in situations where the compiler is able to determine the input to SignedSaturate at compile time, a pure C implementation will be entirely evaluated at compile time. The only code that will be generated will be that required to load the result value into a register. In contrast, an intrinsic function for SSAT will always generate an SSAT instruction because the compiler treats an intrinsic function as a black box, and does not have an operational semantics for it.
2. Static initializer: because it can be evaluated at compile time, a pure C function can be used to initialize a constant. An intrinsic function cannot be used in a static initializer. In the real project, their compiler required an intrinsic function to generate SSAT and they used their saturating macro in the construction of static initializers. To implement what would have been a very significant optimization, they would have needed two macros, one that could be evaluated at compile time, and one that could be efficiently compiled into run-time code. This would have required many changes and was deemed too costly to implement at a relatively late stage in its life cycle.

Likelihood hints

I was unable to find a small illustration of these effect without making the example very contrived, with NOPs. If you can find small examples that are more realistic, I would be very happy to insert them here and credit you.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int Func1( int x )
{
    if( x < 0 )
    {
        x *= (x / 2);
    }
    else
    {
        __asm( "nop" );
    }

    __asm( "nop" );
    __asm( "nop" );

    return x;
}

When it is decided that the benefit of a branch outweighs the cost, there is still an opportunity to make the generated code take fewer branches. Unless branch prediction fails, a not-taken branch (e.g. CBZ r0 when r0 is not zero) allows the processor to exploit all its hardware acceleration for straight-line code. We just need a way to tell the compiler when one outcome is much more likely that another, which can be done with the GCC extension __builtin_expect. CLANG also supports this, and some other compilers support the concept using their own syntax. By convention, these are wrapped in LIKELY and UNLIKELY macros, to make the code more readable.

The compiler can use this information to change a CBZ r0 instruction to CBNZ r0, swapping the generated code at the taken and not-taken destinations. Even when the likelihood hint does not change the conditional jump (because the compiler heuristics already has the likely case at the not-taken destination), we can see that the compiler re-orders the following code to try to minimize taken branches on the likely path.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#define LIKELY( condition_ )   ( __builtin_expect( ( condition_ ), 1 ) )
#define UNLIKELY( condition_ ) ( __builtin_expect( ( condition_ ), 0 ) )

int Func2( int x )
{
    if( UNLIKELY( x < 0 ) )
    {
        x *= (x / 2);
    }
    else
    {
        __asm( "nop" );
    }

    __asm( "nop" );
    __asm( "nop" );

    return x;
}

Conclusion

In these three articles, we have looked at

• the special importance of branchless code when code is executed directly from flash memory,
• how modern compilers can generate branchless object code, also where the high-level code contains conditional if constructs, and
• what we can do at the source level to help the compiler minimize taken branches on our most critical code paths.

In nearly all cases, the most appropriate way to write code is the most natural, readable and maintainable style. Only in the tiny fragments of code that are extremely frequent, or where jitter is critical, we can look into the generated code and massage the source code to minimize taken branches. And when we do that, we can make significant improvements purely by focussing on the number of taken branches.